Nierówności kwadratowe

1️⃣ Czym jest nierówność kwadratowa?

Nierówność kwadratowa to wyrażenie postaci:

• $ax^2 + bx + c < 0$
• $ax^2 + bx + c \le 0$
• $ax^2 + bx + c > 0$
• $ax^2 + bx + c \ge 0$

gdzie $a \ne 0$.

---

2️⃣ Metoda rozwiązania – krok po kroku

Aby rozwiązać nierówność kwadratową, wykonaj poniższe kroki:

1. Wyznacz miejsca zerowe funkcji kwadratowej
   Rozwiąż równanie:
   $ax^2 + bx + c = 0$

2. Narysuj szkic wykresu funkcji kwadratowej
   Parabola ma ramiona:

   • skierowane w górę, jeśli $a > 0$
   • skierowane w dół, jeśli $a < 0$

3. Odczytaj rozwiązanie z wykresu

   • Dla $< 0$ – szukasz, gdzie wykres jest poniżej osi OX
   • Dla $\le 0$ – poniżej lub na osi OX
   • Dla $> 0$ – powyżej osi OX
   • Dla $\ge 0$ – powyżej lub na osi OX

   

---

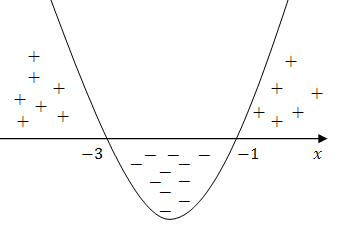
✏️ Przykład 1

Rozwiąż nierówność:
$x^2 + 4x + 3 < 0$

Krok 1: Miejsca zerowe
Obliczamy deltę:

• $\Delta = 4^2 - 4 \cdot 1 \cdot 3 = 16 - 12 = 4$
• $\sqrt{\Delta} = 2$

Miejsca zerowe:

• $x_1 = \frac{-4 - 2}{2} = -3$
• $x_2 = \frac{-4 + 2}{2} = -1$

Krok 2: Wykres
Parabola ma ramiona skierowane w górę, bo $a = 1 > 0$.

Odpowiedź:
Parabola jest poniżej osi OX pomiędzy miejscami zerowymi:
$x \in (-3,\; -1)$

---

✏️ Przykład 2

Rozwiąż nierówność:
$x^2 + 4x + 3 \ge 0$

Te same miejsca zerowe: $x = -3$ oraz $x = -1$

Parabola ma ramiona w górę.

Odpowiedź:
Wykres jest większy lub równy zero poza miejscami zerowymi:
$x \in (-\infty,\; -3] \cup [-1,\; +\infty)$

---